We'll have 2 null objects in the scene that will define the corners of a box. Just like the clicks in creating a rectangle with the marquee tool, the first null defines the origin, and the other is the direction the box goes in. Take this as an exercise in understanding how expressions work with different properties, and hey, you could learn something useful.
So, let's figure this out.
Can I do this with keyframes?
YES! We could animate a mask to do exactly what we need if this were a simpler scenario, however the easiest way to implement marching dots along the line is to use the Dashes feature inside Shape Layers. Plus we also like expressions...
How's it going to work?
I intend to use 2 nulls and a shape layer to create the rectangle. The first Null will be the Upper-Right (UR) corner, the other will be the Lower-Left (LL).
Generally this is all you need to define a rectangle.
Setup the Comp
Create a new comp (1920 x 1080) and add two Nulls and a Shape Layer. Let's name them and change their layer colors so we can differentiate them:
I'm a fan of shape layers, most times they're pretty useful in situations where a Solid would be troublesome, but the opposite also applies. In this case, the Stroke feature will be particularly useful when creating the selection box.
In the BOX layer, let's Add a rectangle and see what we can do with it:
I like the "Add" button. This adds it right in the center of the shape layer and I can move down the chain adding features as I need them, such as Stroke, since we'll need to see the rectangle in order to proceed. Feel free to change its properties as you like.
Positioning
The first task to tackle is to get the Position of the rectangle to follow the two nulls. We know we're going to be referring to the two layers a lot, so it's a good idea to create the Variables first:LL=thisComp.layer("LL").transform.position;
UR=thisComp.layer("UR").transform.position;
We have the two vectors defined by the positions of the 2 null objects. If you remember your vector math , we should be looking at a diagram like this:
What we want to do is put our Shape Layer in the middle of "C".
Vectors are pretty simple. The vector B is represented by LL's position. The vector B+C is represented by UR's position. If we subtract LL from UR (B+C-B) we automatically get C. With that vector, we can divide by 2 to get the center point.
This means we can simply type this into the Position of the Shape Layer, NOT THE RECTANGLE:
(LL+UR)/2
Adding the two figures together and dividing by 2 will give the point directly in between them. So if we move the nulls:
You can probably do some really cool things with this.
Tying the edges
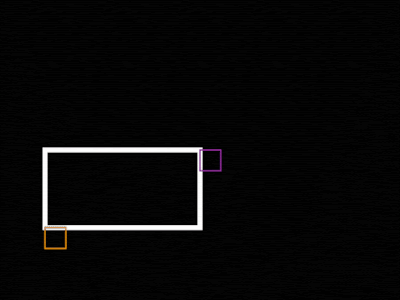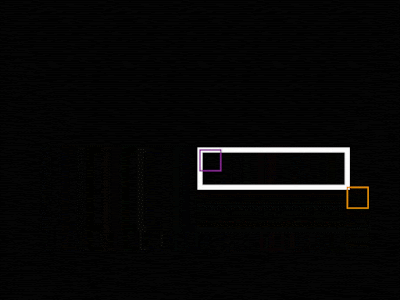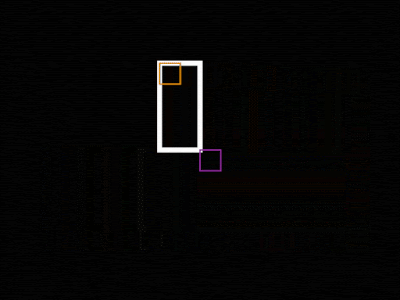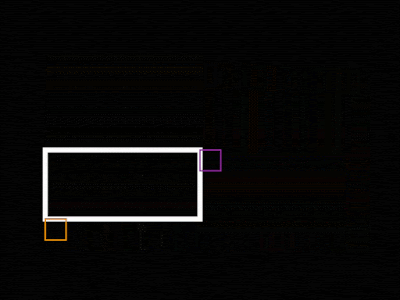
Okay, now we need to figure out the expression to place in "Size" that will make the box fit between the two Nulls. First, place the UR in the upper right section of the comp, then LL in the lower left, just to be sure everything is going as planned.
In order to get the appropriate size of the box, we need to measure the distances between each Null in X & Y then translate that to Size. So, the size would generally be the furthest Null minus the closest relative to the comp. (Check the vectors diagram again). Let's give this a try by applying:
UR-LL
What? That's not right. Well, at least one dimension is right, the X. Let's move the Nulls and see what happens:
Okay, it seems to be working okay when we place them like this. Although this is probably the setup we want since marquee draws using Upper-Left and Lower-Right to orient the rectangle, why isn't it behaving correctly? Let's take a look at the math happening inside the expression:
In the second arrangement, UR is at [1322,904] and LL is at [406,442].
If we subtract these we get [916,462];
Now, moving the Nulls back to where they were in the first arrangement.
UR is at [1172,214] and LL is at [380,712]
If we subtract these we get [792,-498]
Let's see what the expression is returning:
We can see the 792 as the line, but the 0 is what's preventing it from fitting vertically. This is because the last value is -482. The size property does not accept negative values and is clamping to 0.
So, in order to do this we'll need to invert the Y axis. We can do this easily by defining another variable:
Box=UR-LL;
[Box[0],-Box[1]]
Adding the Minus sign in front of the Box makes it immediately reverse whatever value it gets. Just as we've seen above, this expression breaks the arrangement we had before. Now it will only work if LL is below and to the left of UR.
But how about making it work in ANY arrangement?
Math.abs
Math.abs() is a simplified version of what we've done up here. If it receives a positive value, it keeps it positive. If it receives a negative value, it makes it positive.
This means that our "Box" size will always receive a positive value. Unfortunately, Math.abs doesn't work with vectors, so we'll have to break up the dimensions:
Box=UR-LL
[Math.abs(Box[0]),Math.abs(Box[1])];
Be careful with the brackets.
Now, with Position moving the object and the 2 nulls defining the size in any direction. Give it a try.
IT WORKS!
Styling and Example Use
Now, we can style the line. I'll start by changing the stroke settings:
Click the + under Dashes to add the dotted lines. I've also added a Time expression (time*120) to "Offset" to create the marching ants effect:
Add an image behind it all:
Duplicate the "Box" layer. We're going to create a matte to grey out and blur the outside of the selection. In the new copy, remove the "Stroke" and add a Fill. Color doesn't matter. Add an Adjustment layer below the new box and set it's Track Matte to "Alpha Inverted Matte". We can then add the Blur, Glow and Brightness & Contrast effects and set them accordingly:
Add some animation to one Null and we get:
To add more styling, we can make a copy of BOX 2 (the matte), add a "Inner Shadow" layer style and set Fill Opacity to 0. Also, add in a Mouse Cursor and parent it to the bottom left moving Null:
With more track mattes and some text layers, we can complete the project with:
Other Shapes
The same expression can be used to handle the "Size" of any other shape, however, what if we wanted a Star / Polygon / Ellipse that sat between the two nulls and retained a 1:1 aspect ratio?
This one is a lot simpler. Stars, Polygons and Ellipses use "Radius" to define their size, which is one dimension as compared to the 2 dimensions we've been dealing with so far.
This time, in order to get the size the object should be we simply need to measure the distance between the two Nulls using the length() expression. However, note that the length between them is going to give the diameter, so divide by 2 to get the radius:
length(LL,UR)/2;
And we're sorted:
Notice that it uses the top-right corner of the Null since this is where the Anchor Point is.
That's it!
Some vector math, Math.abs() and length() later and we have created a dynamic object that can be interpolated for any use. I hope you learnt something new!